Discover the Path to Mathematical Mastery
An Education That Counts
A sequence is a discrete function \(\boldsymbol a_n\) whose domain is \(\mathbb{Z}\) (i.e. the set of integers). The arguments of a sequence are denoted by subscripts instead of using the typical function notation.

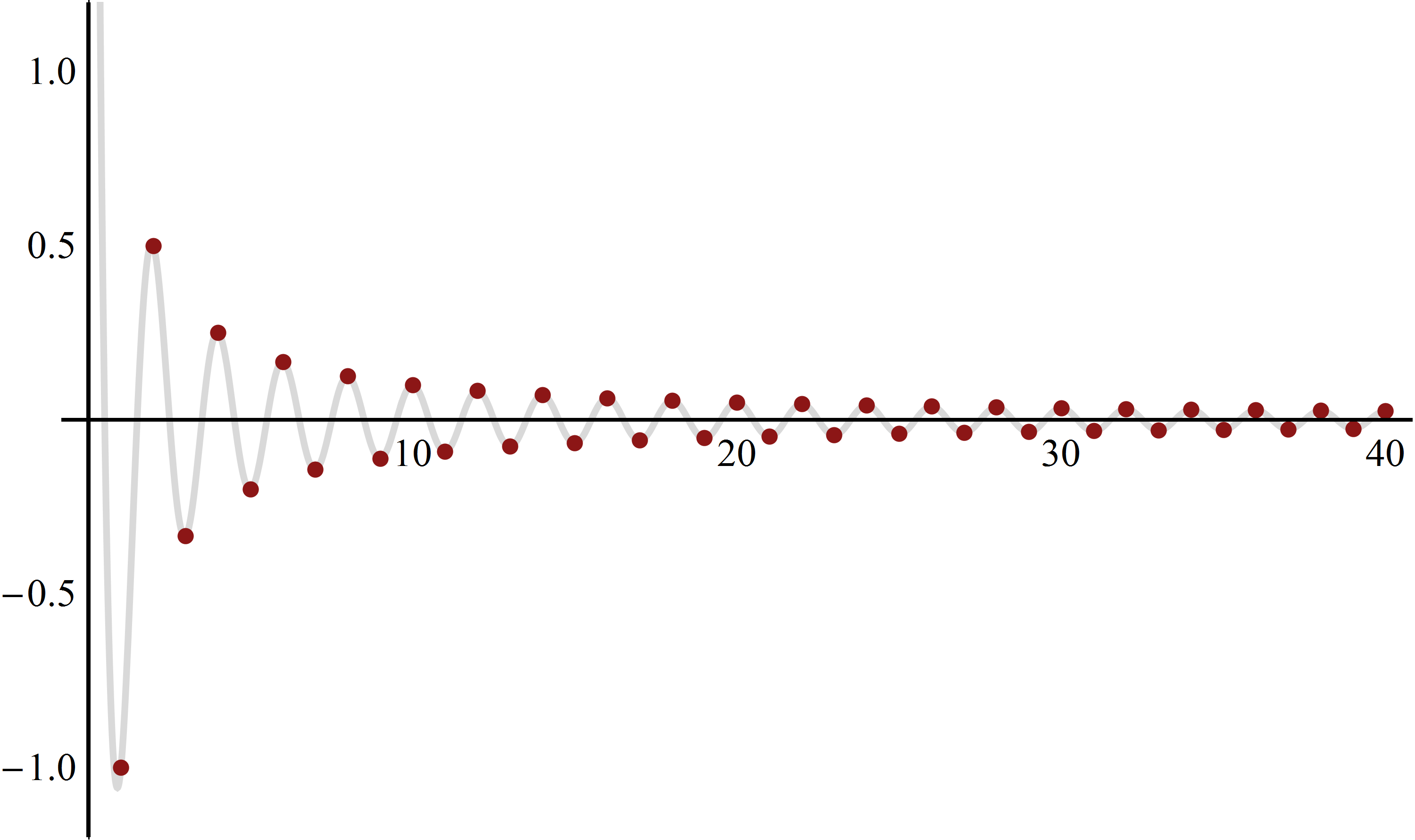 | 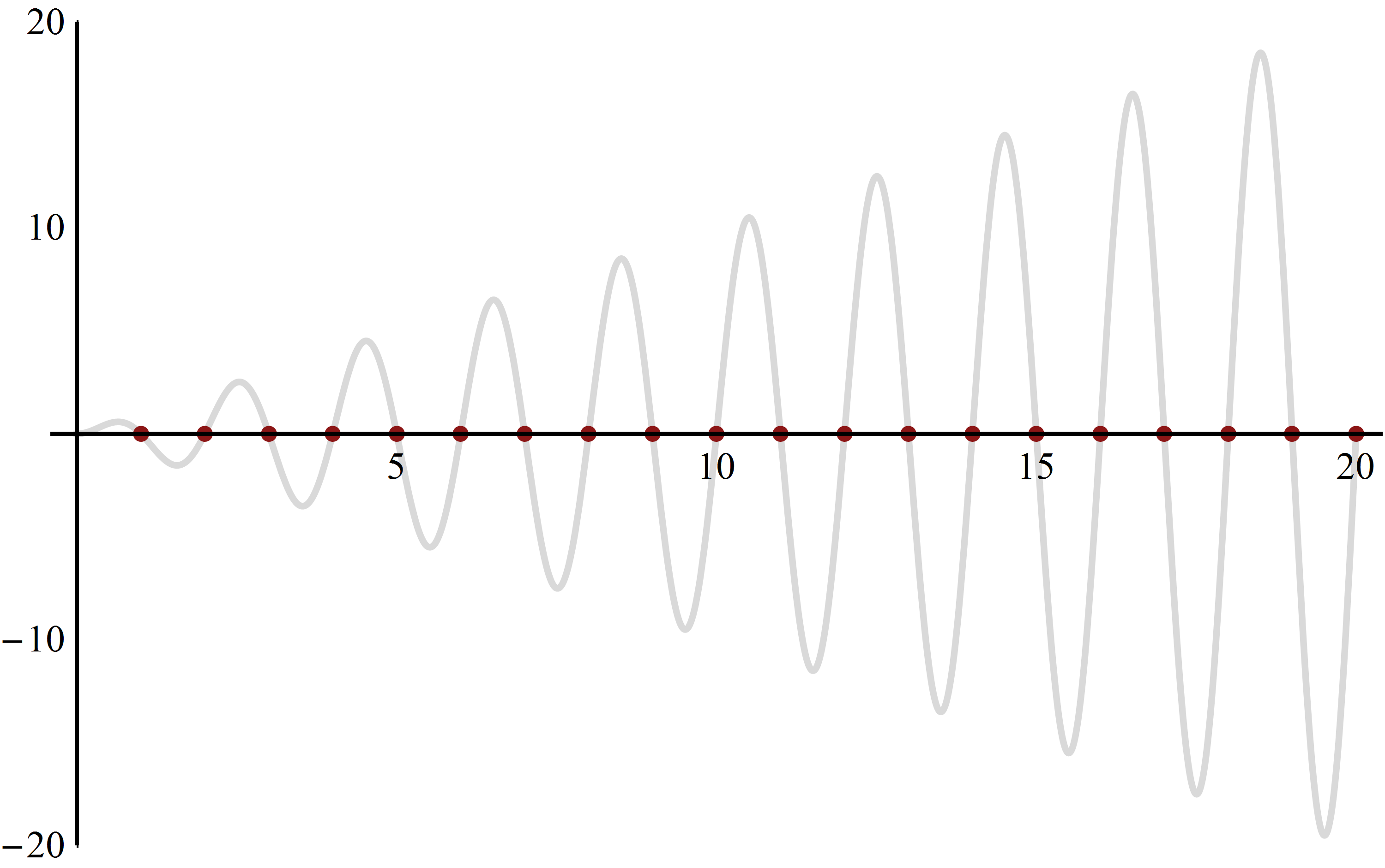 |
A series is a type of (recursive) sequence whose terms correspond to the sum of another sequence of terms \(a_n\). The differences between a sequence and a series can sometimes be mere semantics.
A finite series (or a partial sum) is a series whose term eventually terminate, i.e., \(\displaystyle S_N=\sum_{n=0}^{N}a_n\), whereas an infinite series is of the form \(\displaystyle S=\sum_{n=0}^{\infty}a_n\) which can also be expressed as a limit of the partial sums.
\(\displaystyle\sum_{n=0}^{\infty}a_n=\underset{N\to\infty}{\lim}\sum_{n=0}^{N}a_n=\underset{N\to\infty}{\lim}S_N\).
Check with your tutor
for additional hours.
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | |||||
OnlineMathTutor.co
All Rights Reserved.