Discover the Path to Mathematical Mastery
An Education That Counts
A function \(f(x)\) is said to be continuous at the point \(x=c\) contained within the interval \((a,b)\) provided that the three conditions hold.
If \(f(x)\) is continuous at \(x=c\), then \(\underset{x\to c}{\lim}f(x)=f(c)\)
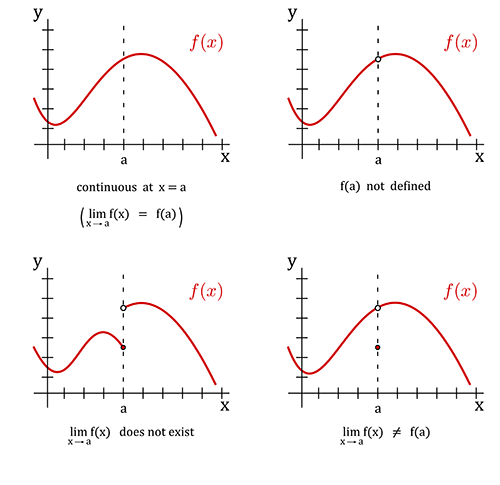
Note: There are some functions such as polynomials, exponentials, cosine, and sine which are continuous everywhere.
Types of Discontinuities
| 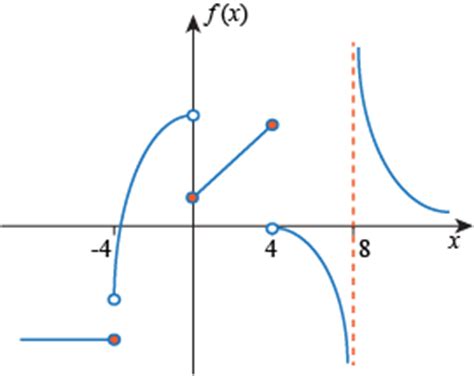 |
| Types of Discontinuities | ||
| Removable | Jump | Infinite |
Intermediate Value Theorem
Let \(f(x)\) be a continuous function on the closed interval \([a,b]\) and let \(N\) be a number such that \(f(a)<N<f(b)\) and \(f(a)\neq f(b)\) then there exists a number \(c\) such that \(a<c<b\) in which \(f(c)=N\)
Intermediate Value Theorem (Corollary)
Let \(f(x)\) be a continuous function on the closed interval \([a,b]\) such that \(f(a)<0<f(b)\) or \(f(b)<0<f(a)\) then there exists a number \(c\) such that \(f(c)=0\)
Continuity
Continuity
Continuity
A function \(f(x)\) is said to be continuous at the point \(x=c\) contained within the interval \((a,b)\) provided that the three conditions hold.
If \(f(x)\) is continuous at \(x=c\), then \(\underset{x\to c}{\lim}f(x)=f(c)\)
Note: Some functions such as polynomials, exponentials, cosine, and sine are continuous everywhere.
Let \(f(x)\) be a continuous function on the closed interval \([a,b]\) and let \(N\) be a number such that \(f(a)<N<f(b)\) and \(f(a)\neq f(b)\) then there exists a number \(c\) such that \(a<c<b\) in which \(f(c)=N\)
Intermediate Value Theorem (Corollary)Let \(f(x)\) be a continuous function on the closed interval \([a,b]\) such that \(f(a)<0<f(b)\) or \(f(b)<0<f(a)\) then there exists a number \(c\) such that \(f(c)=0\)
Check with your tutor
for additional hours.
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | |||||
OnlineMathTutor.co
All Rights Reserved.