Discover the Path to Mathematical Mastery
An Education That Counts
Discover the Path to Mathematical Mastery
An Education That Counts
Calculus is a branch of mathematics that studies motion and how things change.
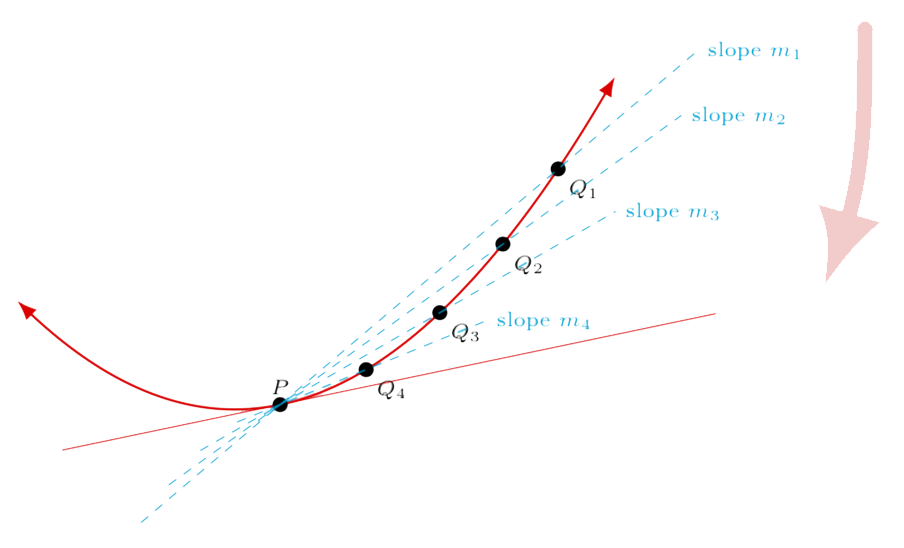
A secant line to a curve is a line that intersects the curve at least at two distinct points. The slope of the secant line at the points \(P(a,f(a))\) and \(Q(b,f(b))\) is found computing the difference quotient
\(\displaystyle m_{secant}=\frac{f(b)-f(a)}{b-a}\)
A secant line can be used to approximate the tangent line to a curve.
The derivative of a function \(f(x)\), which is synonymous with the instantaneous rate of change (or simply rate of change), is defined as follows
\(\displaystyle\underset{h\to 0}{\lim}\frac{f(x+h)-f(x)}{h}=f'(x)\)
The derivative of a function \(f(x)\) at a given value \(x=a\) is defined as follows
\(\displaystyle\underset{b\to a}{\lim}\frac{f(b)-f(a)}{b-a}=f'(a)\)
The difference quotient for a function \(f(x)\) is defined as the function
\(F(x)=\displaystyle\frac{f(x+h)-f(x)}{h}\)
As you perform the following steps simplify as you go.
| Compute the composition: | \(\displaystyle f(x+h)=\) |
| Compute the difference: | \(\displaystyle f(x+h)-f(x)=\) |
| Compute the quoitent: | \(\displaystyle\frac{f(x+h)-f(x)}{h}=\) |
The average rate of change measures how a function \(f(x)\) is changing on from a point \(P\big((a,f(a)\big)\) to point \(Q\big(b,f(b)\big)\)
\(m=\displaystyle\frac{f(b)-f(a)}{b-a}\)
which may be expressed as follows where \(b=a+h\)
\(m=\displaystyle\frac{f(a+h)-f(a)}{a}\)
The average rate of change corresponds
to the slope of a secant line.
The instantaneous rate of change measures how a function \(f(x)\) is changing at a moment’s notice at a given point \(P\big((a,f(a)\big)\).
\(f'(a)=\displaystyle \underset{h\to 0}{\lim}\frac{f(a+h)-f(a)}{h} =\underset{b\to a}{\lim}\frac{f(b)-f(a)}{b-a}\)
The instantaneous rate of change
corresponds to the slope of a tangent line.
Differential functions are ALWAYS continuous functions, but continuous may not be differentiable. Functions that are not differentiable at \(x=a\) means that the slope of the tangent line is undefined at the point \((a,f(x))\). This phenomenon can occur at sharp corners, cusps, discontinuities, or vertical tangent lines. [A cusp occurs when the two different one-sided limits in the limit definition of a derivative yield different values.]
\(\displaystyle\frac{f(x+h)-f(x)}{h}\)
The average rate of change measures how a function \(f(x)\) is changing on from a point \(P\big((a,f(a)\big)\) to point \(Q\big(b,f(b)\big)\)
\(m=\displaystyle\frac{f(b)-f(a)}{b-a}\)
which may be expressed as follows where \(b=a+h\)
\(m=\displaystyle\frac{f(a+h)-f(a)}{a}\)
The instantaneous rate of change measures how a function \(f(x)\) is changing at a moment’s notice at a given point \(P\big((a,f(a)\big)\).
\(\displaystyle \underset{h\to 0}{\lim}\frac{f(a+h)-f(a)}{h}\)
The derivative of a function \(f(x)\), which is synonymous with the instantaneous rate of change (or simply rate of change), is defined as follows
\(\displaystyle\underset{h\to 0}{\lim}\frac{f(x+h)-f(x)}{h}=f'(x)\)
The derivative of a function \(f(x)\) at a given value \(x=a\) is defined as follows
\(\displaystyle\underset{b\to a}{\lim}\frac{f(b)-f(a)}{b-a}=f'(a)\)
Check with your tutor
for additional hours.
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | ||||
OnlineMathTutor.co
All Rights Reserved.
