Discover the Path to Mathematical Mastery
An Education That Counts
…
…
…
Need some additional help understanding how to apply this differentiation technique? Click Here to visit the virtual lesson section.
Answer the following questions in regards to determining the optimized solution.
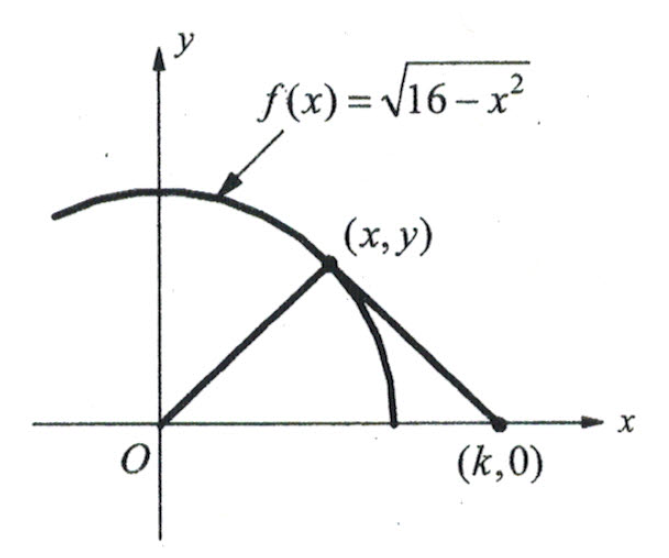
Check with your tutor
for additional hours.
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | |||||
OnlineMathTutor.co
All Rights Reserved.