Menu
Discover the Path to Mathematical Mastery
An Education That Counts
Menu
Discover the Path to Mathematical Mastery
An Education That Counts
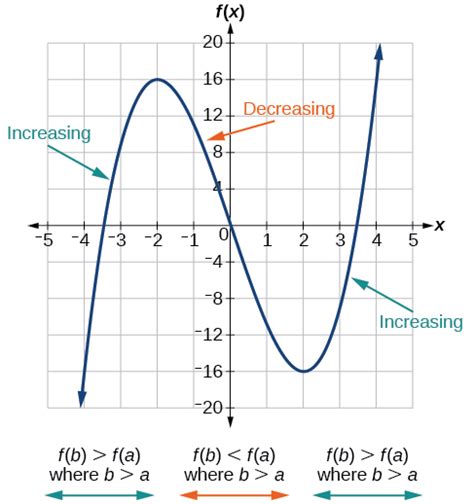
Another valuable application of the derivative involves analyzing the graph of a given function in terms of monocity, concavity, and optimization.
 |
|
A critical point is a point on a graph \(f(x)\) in which the monotonicity of the graph changes. A critical point for \(f(x)\) can be found by finding the critical values for \(f'(x)\).
In other words, if \(c\in(a,b)\) such that \((c,f(c))\) is either a relative extrema then
| Monotonicty and the First Derivative |
|
If the multiplicity of \(c\) is even then there is no change in the monotonicity at \(x=c\).
An inflection point is a point on a graph \(f(x)\) in which the concavity of the graph changes. An inflection point for \(f(x)\) can be found by finding the critical values for \(f'(x)\).
In other words, if \(c\in(a,b)\) such that \((c,f(c))\) is an inflection point then one of the following must hold true.
| Concavity and the Second Derivative |
|
Observe that this analysis upon the second derivative is merely the first derivative test applied to the first derivative of \(f(x)\)
If the multiplicity of \(c\) is even then there is no change in the concavity at \(x=c\).
Check with your tutor
for additional hours.
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
OnlineMathTutor.co
All Rights Reserved.
