Discover the Path to Mathematical Mastery
An Education That Counts
| Average Rate of Change |
The average rate of change of a function \(f(x)\) over a given interval \([a,b]\) measures the average rate of change in the function from the point \(P(a,f(a))\) to the point \(Q(b,f(b))\). The average rate of change is also referred to as the slope of the secant line. \(\displaystyle\begin{align*} m_{\text{Secant}}&=\frac{f(b)-f(a)}{b-a}\\[5pt]&=\frac{\text{Change in } y}{\text{Change in }x}\\[5pt]&=\frac{\Delta y}{\Delta x}\end{align*}\) |
| Instantaneous Rate of Change |
The instantaneous rate of change of a function \(f(x)\) over a given interval \([a,b]\) measures how the function is changing at a moment’s notice. The instantaneous rate corresponds to the limit of the average rate of change from point \(P(a,f(a))\) to point \(Q(b,f(b))\). The instantaneous rate of change is also referred to as the slope of the tangent line at point \(P(a,f(a))\). \(\displaystyle\begin{align*} m_{\text{Tangent}}&=\underset{h\to 0}{\lim}\frac{f(a+h)-f(a)}{h}\\[5pt]&=\underset{Q\to P}{\lim}\big(\text{Ave. Rate of Change}\big)\end{align*}\) |
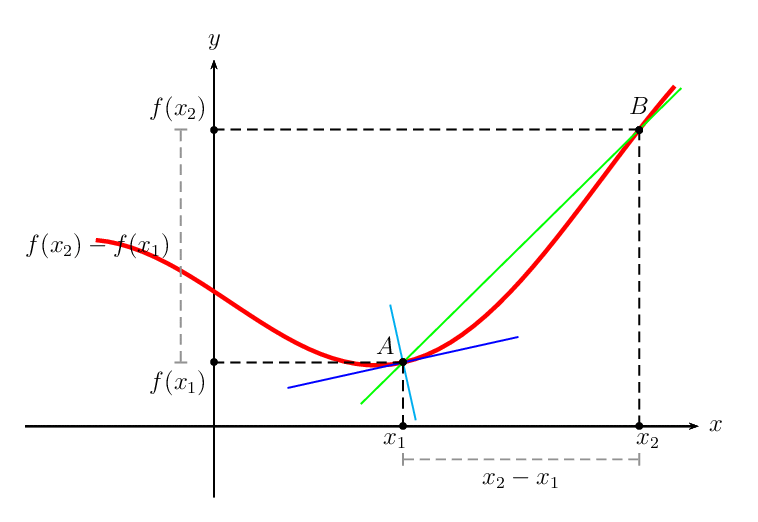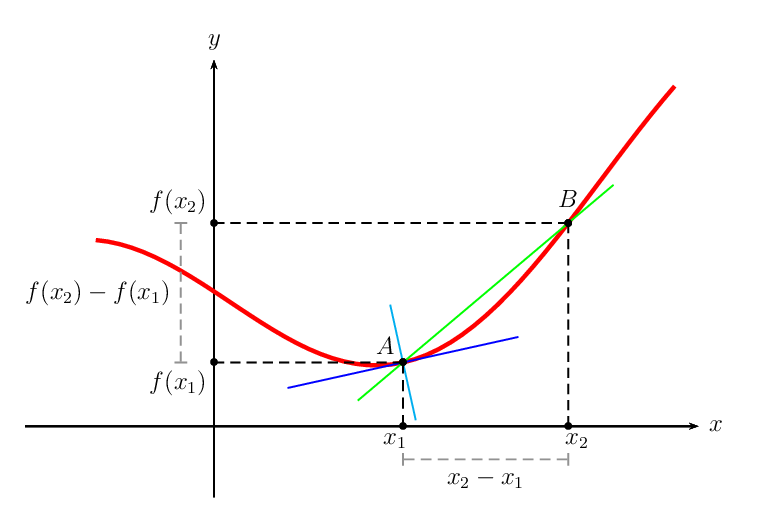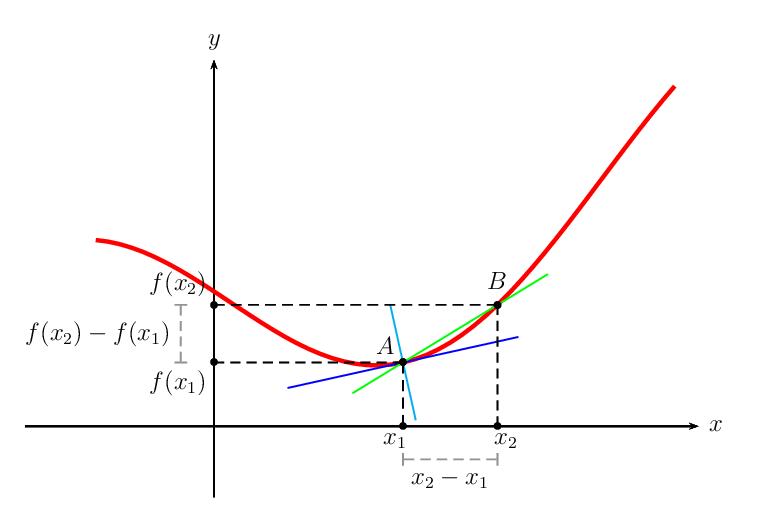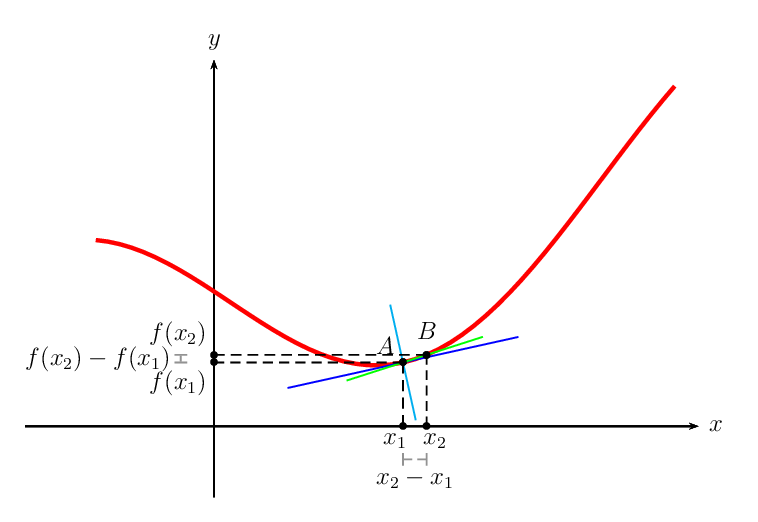
To determine the equation of the tangent line on a given \(f(x)\), note that a tangent line is a LINE. Consequently, the equation of the tangent can be found by updating the point-slope equation \(y-y_0=m(x-x_0)\). Recall that the point \((x_0,y_0)\) must reside on the tangent line, whereas the slope of the line can be found by evaluating the derivative of \(f(x)\) at the given point.
|
The linear approximation (tangent line approxiaiton) for a function \(f(x)\) at the center of \(x=a\) is the tagent line
\(L(x)=f(a)+f'(a)(x-a)\)
Linear approximations are sometimes formulated in terms of differentials such as \(dt\) where \(dy=f'(x)dx\). Applications that require an investigation of incremental changes may require anaylizing the difference \(\Delta y=f(x+\Delta x)-f(x)\)
Optimization problems naturally arise when there is a need to determine the most efficient usage of resources. Common applications included determining the maximizing area that can be enclosed by using a given amount of fencing material, as well as minimizing costs for manufacturing objects from raw material.
A critical number of a function \(f(x)\) is a number \(c\) that is contained within the function’s domain such that either \(f'(c)=0\) or \(f'(c)\) does not exist (DNE).
| First Derivative Test |
Let \(f(x)\) be a function continuous on the open interval \((a,b)\) where \(c\) is a critical value for the \(x\)-coordiante such that \(a<c<b\). Further presume that \(f(x)\) is differentiable at all points of [latexl](a,b)[/latex] except possibly at \(c\). Then
|
| Second Derivative Test |
Let \(f(x)\) be a differntiable function on the open interval \((a,b)\) where \(c\) is a critical value for the \(x\)-coordiante. Furthermore suppose that \(f”(c)\) exists.
|
Relative Extrema
To determine the relative extrema for a function \(f(x)\) on an open interval \((a,b)\)
Absolute Extrema
To find the absolute extrema for a function \(f(x)\) on a given closed interval \([a,b]\) requires determining the relative extrema and insepcting the endpoints.
CAUTION: The \(x\)-value for the critical point is NEITHER the relative extrema NOR the absolute extrema. This \(x\)-value however tell us where to find these extrema values, just as compass points us in the direction of travel. The extrema values for a function corresponds to the \(y\)-value in the critical point, i.e. value for \(f(c)=y\).
Another useful application of the derivative involves analyzing the graph of a given function in terms of monocity, concavity, as well as optimization.
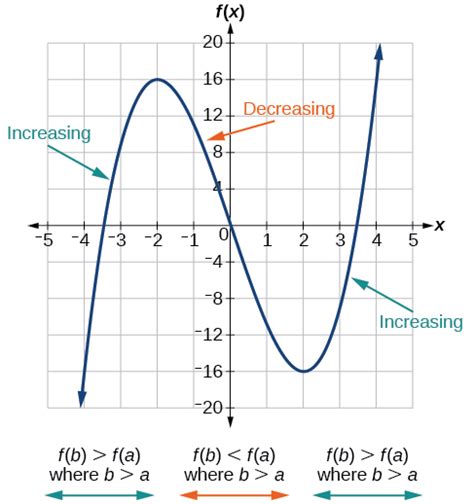 |
|
| Monocity and the First Derivative |
|
An inflection point is a point on a graph \(f(x)\) in which the concavity of the graph changes. An inflection point for \(f(x)\) can be found by finding the critical values for \(f'(x)\). In other words, if \(c\in(a,b)\) such that \((c,f(c))\) is an inflection point then one of the following must hold true.
| Concavity and the Second Derivative |
|
Related rates an application of implicit differential whose variable of differentiation is typically in terms of time \(t\). These problems, as the name suggests, relate various rates by analyzing differentials.
To solve these problems,
| Function | Interpretation | Polarity \(v(x)\) | Polarity \(a(x)\) | Motion | |
| \(f(x)\) | Position | \(v(x)<0\) | \(a(x)<0\) | Speeding Up | |
| \(v(x)=f'(x)\) | Velocity | \(v(x)<0\) | \(a(x)>0\) | Slowing Down | |
| \(\begin{align*}a(x)&=v'(x)\\&=f”(x)\end{align*}\) | Acceleration | \(v(x)>0\) | \(a(x)<0\) | Slowing Down | |
| \(v(x)>0\) | \(a(x)>0\) | Speeding Up |
A particle changes direction whenever \(v(t)=0\)
When the object is moving in the
The Total Distance for an object from \(x=a\) to \(x=b\) whose velocity is given by \(v(t)\) can be found by evaluating the integral \(\displaystyle \int_{a}^b|v(t)|dt\).
Displacement measures the net change of the object’s position, which can be found by computing \(\displaystyle \int_{a}^b v(t)dt\). Notice the subtle difference between these integral. When is it guaranteed that the total distance travel is the same as the displacement?
| Mean Value Theorem | ||
Let \(f(x)\) be a function that satisifes the two conditions
Then, there exists a number \(c\) within the interval, i.e. \(a<b<c\), such that the following holds true \(\displaystyle f'(c)=\frac{f(b)-f(a)}{b-a}\)
|
| Rolle’s Theorem |
|
If \(f(x)\) is a function continuous on the closed interval \([a,b]\) and differentiable on the open interval \((a,b)\) such that \(f(a)=f(b)\) then there exists at least one \(c\in(a,b)\) in which \(f'(c)=0\) 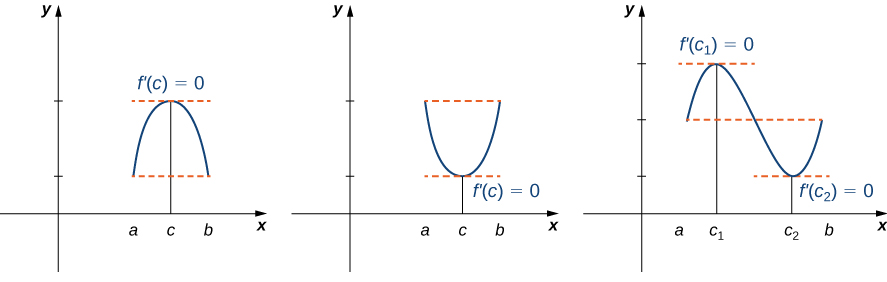 |
To determine whether a function \(f(x)\) is invertible over a given region it must pass the horizontal line test. Functions that pass the horizontal line do not change in their monocity, in other words, either \(f'(x)>0\) always or \(f'(x)<0\) always.
What happens if the monocity of a function changes?
To determine the equation of the tangent line on a given \(f(x)\), note that a tangent line is a LINE. Consequently, the equation of the tangent can be found by updating the point-slope equation \(y-y_0=m(x-x_0)\). Recall that the point \((x_0,y_0)\) must reside on the tangent line, whereas the slope of the line can be found by evaluating the derivative of \(f(x)\) at the given point.
|
Another useful application of the derivative involves analyzing the graph of a given function in terms of monocity and concavity.
First Derivative Test Let \(f(x)\) be a differentiable function on a given interval \((a,b)\)| Function | Interpretation | Polarity of \(v(x)\) | Polarity of \(a(x)\) | Object’s Motion | |
| \(f(x)\) | Position of a particle | \(v(x)<0\) | \(a(x)<0\) | Speeding Up | |
| \(v(x)=f'(x)\) | Velocity of a particle | \(v(x)<0\) | \(a(x)>0\) | Slowing Down | |
| \(a(x)=v'(x)=f”(x)\) | Acceleration of a particle | \(v(x)>0\) | \(a(x)<0\) | Slowing Down | |
| \(v(x)>0\) | \(a(x)>0\) | Speeding Up |
CAUTION: The \(x\)-value for the critical point is NEITHER the relative extrema NOR the absolute extrema. This \(x\)-value however tell us where to find these extrema values, just as compass points us in the direction of travel. The extrema values for a function corresponds to the \(y\)-value in the critical point, i.e. value for \(f(c)=y\).
\(\displaystyle f'(c)=\frac{f(b)-f(a)}{b-a}\)
Check with your tutor
for additional hours.
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | |||
OnlineMathTutor.co
All Rights Reserved.