Discover the Path to Mathematical Mastery
An Education That Counts

Important Definitions and Concepts
A mapping is a rule that correlates elements, which can be expressed in terms of an ordered pair such as \(R=\{(1,2),(2,3),(4,5)\}\).
Mappings that have exactly one output for each input are known as functions.
A function is a type of mapping \(f:A\mapsto B\) in which there is EXACTLY one output for each input.
The vertical line test is a graphical means to determine if a mapping is a function. This test states that if a vertical line intersects a graph at least twice, then the mapping is NOT a function. In other words, a mapping is a function provided that each vertical line intersects a graph at most once.
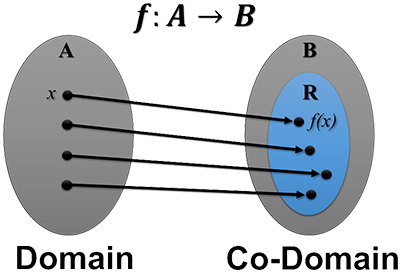
| Terminology | Definition |
| Domain | The domain of a function is the set of all input values. In the diagram above, the domain is set \(A\). Input values are typically expressed in terms of \(x\) values, but not always. |
| Co-Domain | The co-domain of a function is the set that contains all output values and any additional values. In the diagram above, the co-domain is set \(B\). |
| Range | The range of a function is the set of all output values. In the diagram above, the range is set \(R\). The range is always a subset of the co-domain, but the converse is not always true. Output values are typically expressed in terms of \(y\) values, but not always. |
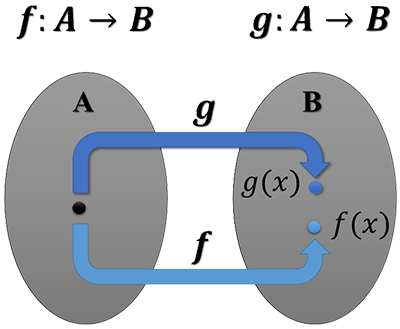
Let \(f:A\mapsto B\) and \(g:A\mapsto C\) be functions.
| Notation | Description |
| \((f\pm g)(x)\) | The notation is used to describe either the sum or the difference \(f(x)\pm g(x)\) |
| \((fg)(x)\) | The notation is used to describe the product \(f(x) \cdot g(x)\) |
| \(\displaystyle \left(\frac{f}{g}\right)(x)\) | The notation is used to describe the quotient \(\frac{f(x)}{g(x)}\) provided that \(g(x)\neq0\) |
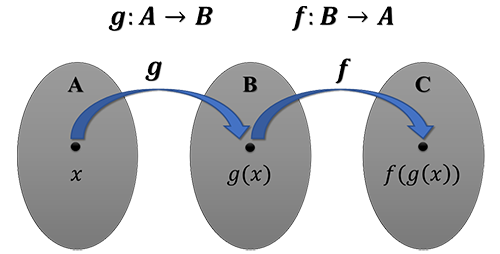
An important type of function notation known as function composition is an essential part of mathematics. Let \(f:A\mapsto B\) and \(g:B\mapsto C\) be functions.
| Notation | Description | ||||||
| \(\big(f\circ g \big)(x)\) | This is the notation that is used to describe function composition in which the outputs of \(g(x)\) are the (potential) inputs for the function \(f(x)\). See diagram above. | ||||||
| \(\big(g\circ f \big)(x)\) | This is the notation that is used to describe function composition in which the outputs of \(f(x)\) are the (potential) inputs for the function \(g(x)\). | ||||||
| \(\displaystyle F(x)=\frac{f(x+h)-f(x)}{h}\) | This particular function composition is known as a difference quotient, which is one of the foundations of calculus.
|
| Function Type | Definition |
| Injective | A function \(f(x)\) is said to be injective, or one-to-one, provided that for each distinct element in the domain, there is a corresponding distinct element in the range. The horizontal line test is a graphical means to determine if a function is injective. This test states that if a horizontal line intersects a graph at least twice, the mapping is NOT a function. In other words, a mapping is a function provided that any horizontal line can only intersect a graph at most once. A given function can be shown to be injective by demonstrating that if the images are the same \(f(a)=f(b)\), then the inputs must also be the same \(a=b\) |
| Function Type | Definition |
| Surjective | A function \(f(x)\) is said to be surjective, or onto, provided that for each element in the co-domain \(b\in B\) there is a corresponding element in the domain \(a\in A\) such that \( f(a)=b\). A function is surjective on a given co-domain \(B\) provided that the range \(R\) is the same, i.e. \( B=R\). A given function can be shown to be subjective by demonstrating for any \(b\in B\) it possible to find an element \(a\in A\) such that \(f(a)=b\). |
| Function Type | Definition |
| Bijective | A function \(f(x)\) is said to be bijective, or a one-to-one correspondence provided that the function is both injective and subjective. |
| Function Type | Definition |
| Invertible | A function \(f(x)\) is said to be invertible, provided that it is bijective for a given domain \(A\) and co-domain \(B\). The inverse of \(f(x)\) is denote as \( f^{-1}(x)\) which is NOT be confused as a fraction, i.e. \(\displaystyle f^{-1}(x)\neq\frac{1}{f(x)}\). An essential characteristic of an invertible function is that the inverse function UNDOES what the function DID.
An inverse may sometimes be found “swapping” \(x\) and \(y=f(x)\) in a given equations, and then solving for \(y\). Some inverses cannot be easily computed. |

Check with your tutor
for additional hours.
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | |||||
OnlineMathTutor.co
All Rights Reserved.